編集部

2025.03.07

『統計学』とは？身近な例や基礎知識、分析手法、経済学との関係について解説します

統計学と聞くと「何か難しいもの」というイメージを持つかもしれません。統計は私たちの生活と密接に結びついているため、近年小学校から高校まで統計教育が取り入れられています。情報化社会が進展し、さまざまなデータが可視化されている現代では、統計学が人生を豊かにするツールの1つになっています。そこで、統計学の魅力と基礎知識について、麗澤大学経済学部の池川先生に解説してもらいました。

近年、学校では「統計教育」に力を入れている

文部科学省が定めている教育課程の基準「学習指導要領」は、およそ10年に1度改訂されています。統計教育は、2017年から小・中・高と順次新学習指導要領の中に盛り込まれ、実施されています。

その中で、理数教育の充実にかかわる項目に「必要なデータを収集・分析し、その傾向を踏まえて課題を解決するための統計教育の充実」が含まれています。こうした背景には、近年のデータサイエンスの進展や、さまざまな場面でデータに基づいた意思決定が重視されるようになったことが挙げられます。

参考「学校における統計教育の位置づけ」（総務省統計局）
https://www.stat.go.jp/teacher/stat-education.html

統計学の身近な例

統計学が身近に使われている例を2つ紹介します。

ソーシャルゲームのカプセルトイにかかる金額と確率

統計学の確率の公理や公式を使えば、「ソーシャルゲームのカプセルトイで、いくら課金すれば☆5が当たるか」がわかるという例を紹介します。

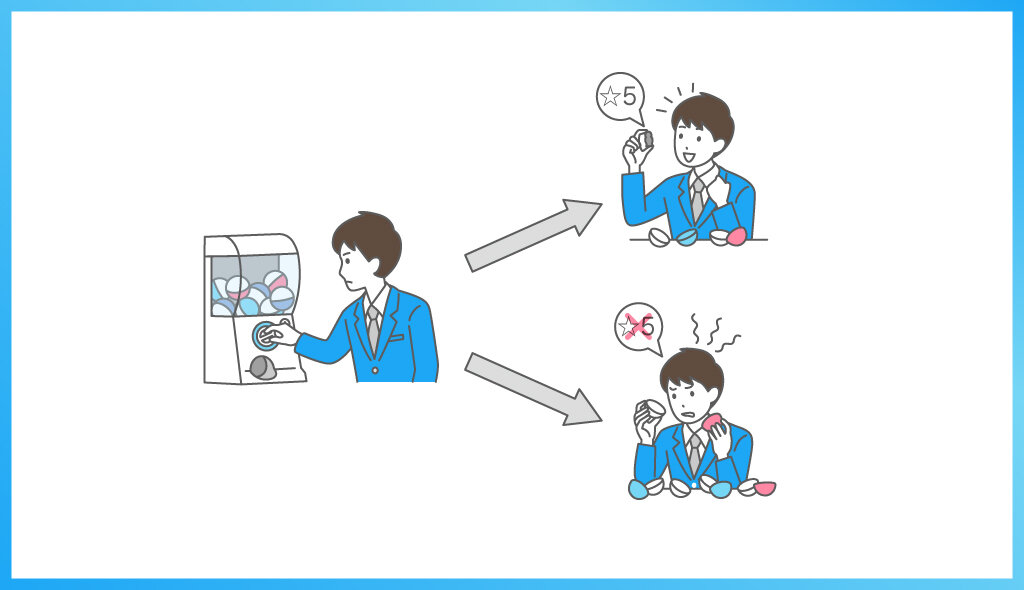
画像①.jpg

確率とは、ある事柄が起こる可能性の頻度（度合い）を指します。カプセルトイは「当たるか当たらないかのどちらか」なので、起こり得る結果が2通りの「二項分布」に当たります。そこで、二項分布の確率の公式を使えば答えを求められます。

今回求めたいのは「90回連続で回して、☆5が1回以上出る確率」です。以下のように、カプセルトイを回す回数を90回、☆5が当たる回数を0回、排出率（1回あたりの当たり確率）を0.6％と仮定して、まず二項分布の確率の公式に当てはめます。

画像②.jpg

■条件

・nはカプセルトイを回す回数

（例えば、90回カプセルトイを回したとすると「n＝90」）

・xは☆5が当たる回数

（今回は1回も出ない確率を求めるので「x＝0」）

・πは1回あたりの当たり確率

（今回は排出率0.6％と仮定すると「π＝0.006」）

公式に当てはめて出した値が、以下になります。

・90回連続で回して1回も出ない確率＝0.58180...

次に、確率の公理に従うと「1回も出ない確率を1から引けば、1回以上出る確率を求められる」ため、引き算します。

・90回連続で回して1個以上☆5が出る確率＝1－0.5818＝0.4182

したがって、90回連続で回して排出率0.6％の☆5が1回以上出る確率は約41.8％であることがわかります。

詳しい解説は、下記の動画をご覧ください。

「文系のためのデータ分析～ソシャゲから地域創生まで～」（夢ナビ）

https://douga.yumenavi.info/Lecture/PublishDetail/2023002523?back=

参考「推測統計」（総務省統計局）
https://www.stat.go.jp/naruhodo/11_tokusei/suisoku.html

参考「中心的な傾向を捉える」（総務省統計局）
https://www.stat.go.jp/naruhodo/5_tokucho/chushin.html　

受験校の目安となる偏差値の仕組み

偏差値は受験校を選ぶときの大切な目安の1つです。例えば、社会の点数が80点、数学の点数が70点だった場合、その得点だけを見て「社会の方が得意」だとはいえません。なぜなら、社会と数学とでは難易度が違うこともあるからです。こういうとき、統計学の標準化という手法を活用すれば、複数のデータを同じ指標で比較できるようになります。

標準化はデータの平均値が0、標準偏差が1になるように変換することです。試験の点数で考える場合の標準化とは、試験を受けた人がとった点数の真ん中に山を持ってくるという考え方です。

通常、テストの成績は平均点の近くに人数が一番多く集まり、0点や100点に近づくほど人数が少なくなり、点数の分布は釣鐘型（つりがねがた）になることが多い傾向があります。このような分布の型を「正規分布」といいます。標準化する前はデータごとに裾が広がった形だったり、真ん中が高くなっていたりと山の形はさまざまなので、標準化することによって山の形が同じになるように整えます。

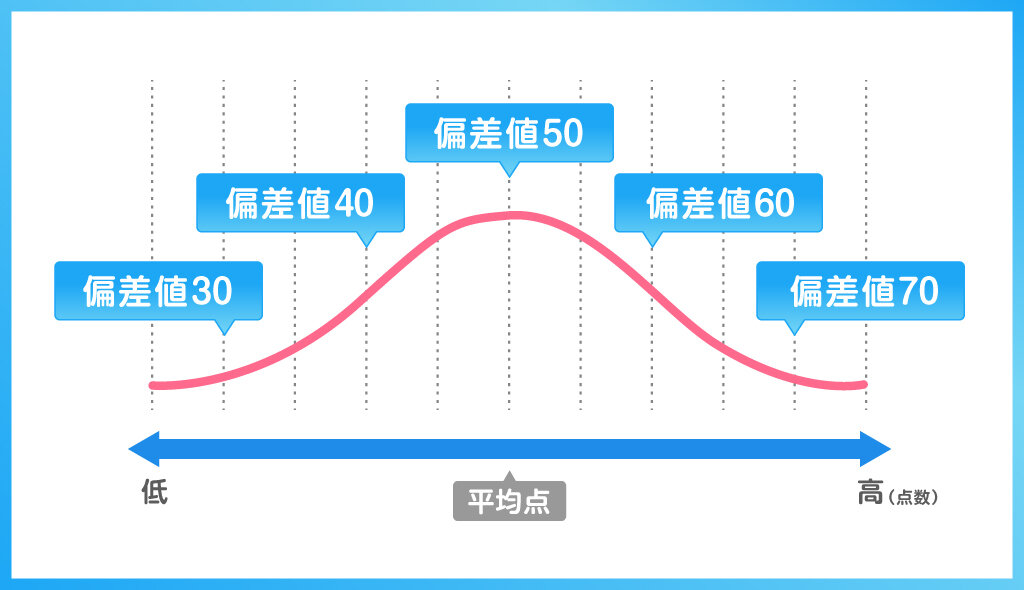
画像③.jpg

そのため、偏差値はテストの成績の分布が正規分布であると仮定して、その真ん中の値を50になるように変換し、テストを受けた中で自分がどれくらいの位置にいるかを数値化したものです。この偏差値を見れば、試験の難易度が異なる教科間でも、同じ指標で比較することが可能になるのです。

統計学の基礎知識

ここでは、統計学の基礎知識について説明します。

統計学とは

統計とは、集団の傾向・性質を数量的に明らかにすることです。総務省統計局では、統計学を「まとめてはかる学問」だとしています。まとめてはかることによって、現状を把握するための記述、現状を左右しうる要因の探索、限られた情報からの予測、特定の要因が本当に原因なのかの検証ができるというメリットがあります。

参考「統計とは？」（総務省統計局）
https://www.stat.go.jp/teacher/statistics.html#what

参考「第1章統計学でできること」（総務省統計局）P4
https://www.stat.go.jp/rikatsuyou/pdf/seminar1-1.pdf

統計学の種類と特徴

統計学は大きく2種類あります。

・記述統計学

記述統計学とは、得られたデータの性質や傾向を明らかにする分野で、平均値や分散、相関係数を扱うものです。

・推測統計学

推測統計学とは、サンプルデータ（標本）から全体（母集団）の状況を推測する学問のことで、順列や確率を扱います。

参考「はじめての統計データ利活用セミナー」（総務省統計局／2022年3月2日）
https://www.stat.go.jp/rikatsuyou/pdf/2022seminar.pdf

統計学と機械学習の違い

統計学と機械学習の違いはどこにあるのでしょうか。機械学習は、コンピュータがデータを読み込むことで自動的にルールやパターンを見出し、その結果を活用して分類や予測を行う仕組み全体のことをいいます。一方、統計学は数学的手法を使ってデータを扱う学問です。

参考「第1章データサイエンス(機械学習のアルゴリズム)によるデータ解析が社会にもたらす変化」P4（総務省統計局）
https://www.stat.go.jp/teacher/dl/pdf/c4learn/materials/fourth/dai1.pdf

よく使われる統計分析の手法・指標

次に、よく使われる統計分析の手法や指標などについて説明します。

平均値

集団の中心的傾向を示す値を「代表値」といいます。平均値は代表値の1つで、変量の総和を個数で割った値です。例えば、試験の平均点はクラス全員の得点を足して、クラスの人数で割って求めます。その平均点がその場合の平均値です。

参考「中心的な傾向を捉える」（総務省統計局）
https://www.stat.go.jp/naruhodo/5_tokucho/chushin.html

分散

分散とは、データ全体の散らばりの程度を測る指標のことをいいます。

参考「データの散らばりを見る」（総務省統計局）
https://www.stat.go.jp/naruhodo/10_tokucho/chirabari.html

相関係数

相関係数とは、相関の強さを表す指標で、-1から1の間の値をとります。2つの変量が正の相関関係にある場合は正の値をとり、負の相関関係にある場合は負の値をとります。

参考「基本用語集（そ）」（総務省統計局）
https://www.stat.go.jp/teacher/glossary-sa-so.html#coefficient-of-correlation

回帰分析

回帰分析とは、複数の変数の因果関係を表すのにもっとも適した線を作成して数式化する分析手法のことです。

参考「複数の変数の関係性を見る」（総務省統計局）
https://www.stat.go.jp/naruhodo/10_tokucho/hukusu.html

統計的因果推論

統計的因果推論とは、物事や事象が起こる因果を調べるための数学的・統計学的方法論を指します。

参考「2.7.3因果推論」P1（科学技術振興機構）
https://www.jst.go.jp/crds/pdf/2022/FR/CRDS-FY2022-FR-04/CRDS-FY2022-FR-04_20703.pdf

確率

ある事柄が起こる可能性の頻度（度合い）のことです。

参考「13統計用語辞典」（総務省統計局）
https://www.stat.go.jp/naruhodo/13_yougo/ka-gyo.html

統計学でできること、できないこと

統計学をツールとして活用すれば、予測や仮説を立てることなどが可能になります。ただし、統計学ではできないこともあります。そこで、できること＝得意なこと、できないこと＝苦手なことに置き換えて、それぞれ具体的に紹介します。

統計学でできること

統計学が得意なことには、以下のようなことが挙げられます。

・わかりやすくまとめること

実際に、学生が行った分析事例を見てみましょう。

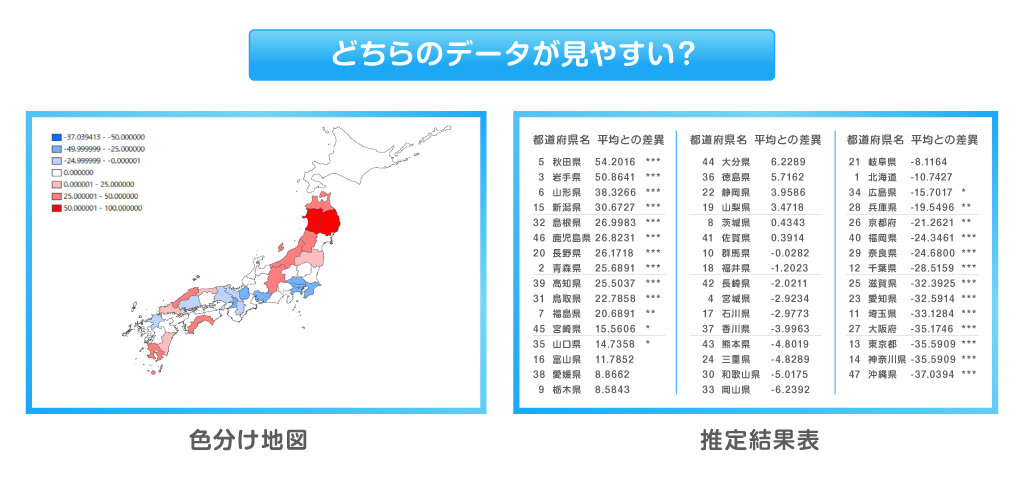
画像④.jpg

上記の図は、統計学を利用して「塩分摂取量が生活習慣病による死亡率にどう関係するか、それに地域差はあるか」について、学生が行った研究です。統計の手法を使って計算すると、結果は右のようなデータが表として出てきます。

この数値を解析しながら仮説検証を進めていくわけですが、表だけを見ても「どの地域で塩分摂取が多いのか」「どの地域が塩分摂取によって死亡率が高いのか」などイメージが湧きません。

そこで、数値結果を落とし込んだものが左の全国地図です。地域ごと「塩分摂取量に起因する生活習慣病の死亡率」や「地域差」などの状況が一目でわかります。これが図示や表などを用いたビジュアライゼーションの効果です。

地図上では岩手県と秋田県が同じ色になっていますが、より詳細に分析する際にはそれぞれのデータを表で確認します。このように目的によって表示手法を使い分けられると、統計学の可能性が広がります。

・予測やシミュレーション、仮説の検証

上記の「都道府県別塩分摂取量と死亡率」の研究を例にして説明します。この研究では、学生が「塩分摂取量が多い、料理の味の濃い地域ほど死亡率が高いのではないか」という仮説を立てました。そして、実際に分析すると仮説どおりの結果となり、統計的にそれが証明されました。これが予測と仮説の検証です。

また、シミュレーションに関しては、以前サブカルチャー好きな学生が「『ウマ娘』が多額のドネーション（寄付）を獲得した」という現象について研究した事例があります。もし「寄付額が全額その地域の産業に割り振られたとしたら、どのくらいの経済効果があるか」というシミュレーション分析です。

このケースでは100％当たるとはいい切れませんが、ある程度の精度でシミュレーションできるのではないかという研究内容でした。データ分析に近いかもしれませんが、シミュレーションも統計学の得意分野です。

・客観的な指標を与えること

統計学で数値を出していれば、客観的な指標として伝えることが可能です。「観光客がすごく増えました」というのと、「10％増えました」というのでは、伝わる情報の質が違います。

「すごく」がどの程度かは人によって解釈が違いますが、パーセンテージを提示すれば、その事実は正確に伝わります。人を納得させる点においては、客観的な数値がプラスに働くことは間違いありません。

統計学でできないこと

次に、統計学の苦手なことについても見ていきましょう。

・質的な事象を可視化すること

統計学は数値データを使いますので、質的な事象を可視化することが苦手です。車好きの学生の研究を例にして説明しましょう。以前、ゴツゴツした車の中古車価格が上がっているという現象があって、それを数値上で分析しました。

その際、ゴツゴツした車を規定するため、空気抵抗値であるCd値を使いました。学生は「その値が大きいほどゴツゴツしている」と考えたわけです。そして、その数値（代理変数）を使って分析すると、いい結果が出ました。

しかし、Cd値を知ってもそれぞれの車のイメージは湧きません。実際に、各車がどの程度ゴツゴツしているか、つまり車の質的な事象は実際に車を見るか、あるいは写真で見るかしないとわかりません。それが統計学の限界の1つです。

・判断すること

シミュレーション分析などを実施して、計算上は「観光客が10％増えた」という数値を出すことは可能です。ただし、その10％増を多いか少ないか、あるいはその数値が正しいかどうかを解釈するのは、データの力だけではできません。

最終的に判断するのは、あくまで人の力です。そして、判断するためには、統計学はもちろんのこと、他の分野の知識や理論が必要になります。

統計学と経済学の関係

経済学部で統計学を学ぶのは、なぜでしょうか。統計学はツールの1つなので、使いこなすには知識が必要です。例えば、計量経済学は経済学の知識や考え方と、統計学のツールとしての側面を活用して経済現象や経済の動きなどを解明する分野です。それは、統計学と経済学の知見の両方を持ち合わせて可能になることです。

ただ、ツールは統計学以外にもあります。調査もツールといえるでしょう。また、ツールも使い方は多様です。目的に応じて、統計学を使うのがふさわしいときに、ふさわしいやり方で活用すれば、経済に関するさまざまな事象を解明することができます。

麗澤大学経済学部が統計学に力を入れる理由

麗澤大学経済学部で統計学に力を入れるのは、経済理論の学びと実践力を発揮して、エビデンスに基づく政策立案・評価できる人材を育成するためです。まず、エビデンスに基づく政策立案とは何でしょうか。その文脈で登場するのは、消費者と企業、そして政府です。

例えば、政府が税金政策を考えるときに、「物価が高くてみんな困っているから、消費税0％にしましょう」というのは、客観的な指標に基づかない単なる思いつきです。その政策を進めてしまっては、税収が足りなくなってしまいます。

税収が足りなくなると、インフラの整備や医療サービスなど現在税金でまかなわれていることが滞る結果に陥ってしまいます。では、税率を何％にすればいいかという場合に、客観的な指標が必要になります。このように政策を考えるときには「コストがどのくらいで、どのようにペイできるか」という指標やエビデンスが、提案や判断の材料として欠かせません。

政策に限ったことではありません。

例えば、営業職について考えてみましょう。自社のサービスを買ってもらうとき、「これを導入していただければ、売り上げがすごくアップします」とセールスしても説得力がありません。「売り上げがこのくらい見込めて、純利益としては10％増加することが推定できます」という提案ができれば、取引先は前向きに購入を検討してくれる確率が上がるはずです。

これは購入する立場でも同じです。「10％増加する」といわれた場合、その10％がコストに対して高いかどうかを正しく判断するには、数値の意味を理解できないと難しいでしょう。また、一消費者として統計学の視点を持てば、危険な商売に騙される心配もありません。

私たちの日常には、統計学を用いて決めたり評価したりすることが潜んでいます。当然ビジネス上でも、統計的なスキルと経済的な視点はさまざまな場面で大いに役立ちます。

統計学の授業を通して身につく力

統計学の授業を通して、経済学部の学生に身につけてほしいスキルはデータを用いて分析・評価する力です。

データを用いて分析・評価する力

私が担当している計量経済学の授業では、入門期から分析テーマを自分で設定してもらい、そのテーマに見合うデータを自分で探したり計算したりした上で、実際に統計分析を行ってプレゼンテーションしてもらいます。

主体的にテーマを考えてもらうと、多くの学生が自分の興味ある分野でテーマを設定します。そうすると、「統計学は難しい」という意識が変化し、統計学へのハードルが下がります。また、最初から学生が主体的に取り組むため、実践的な経験を通してデータを使って分析する力、評価する力が身につきます。

ただ単に興味のある分野でデータを活用することだけにとどめると、経済学として実践的な学びにはつながりません。そのため、例えば、ゲームがテーマの場合はゲームの市場にまで対象を広げ、経済学寄りのテーマに近づけながら学生とともに応用したり発展させたりしていきます。そうすれば、統計学を生かした経済学の分野として深く学ぶことができます。

麗澤大学公式サイト「これからの経済社会に求められる人材へ　経済学部」（麗澤大学）
https://www.reitaku-u.ac.jp/faculty/economics/